Modelo SIR
Published:
Código do modelo está disponível no GitHub neste link sob MIT License.
Por volta de 1760, Daniel Bernoulli procurou verificar a eficácia das políticas públicas para o tratamento da varíola através de um modelo matemático. Bernoulli em seu modelo usou conceitos do cálculo diferencial, e descreveu a variação do número de indivíduos “Suscetíveis”, que nunca tinham sido contaminados por varíola no tempo t, e dos indivíduos “Recuperados” [Bacäer,2001].
Posteriormente no século XX, McKendrick e Kermack elaboraram o modelo compartimental com equações diferencias, que chamaram de SIR, que classifica os indivíduos em três estados: (S)uscetíveis, (I)nfectados e (R)ecuperados; que pode ser definido por um sistema de equações diferencias ordinárias, apresentadas na imagem abaixo. As letras gregas $\beta $ e $\nu $ são constantes positivas e caracterizam a interação entre o agente infeccioso e a população. Mais explicitamente $\beta $ é a proporção de indivíduos suscetíveis que se tornarão infectados e $\nu $ é a proporção de indivíduos infectados que se recuperarão. Assume-se que as três classes estão uniformemente distribuídas pelo espaço. Assim, as taxas de encontro independem da localização geográfica, o que permite modelar esse sistema por meio de equações diferenciais ordinárias. Além disso, a população total permanece constante [Edelstein-Keshet,2005].
Sistema de EDOs e Fluxograma
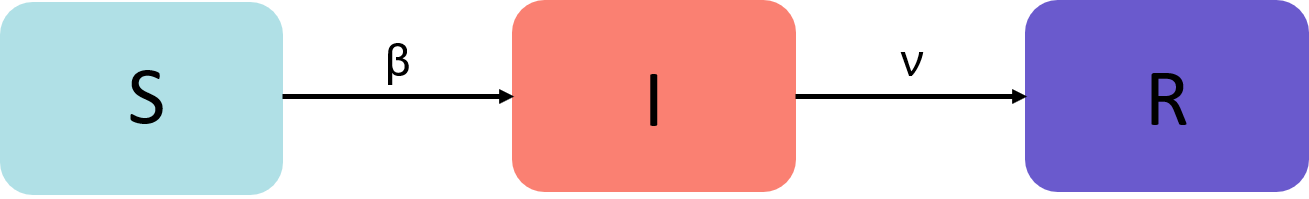
$$\begin{cases} \frac{dS}{dt}=-\beta S\frac{I}{N};\\ \frac{dI}{dt}=\beta S\frac{I}{N} - \nu I;\\ \frac{dR}{dt}=\nu I; \end{cases} $$ Sendo, $N=S+I+R$ a população total.
McKendrick e Kermack, em 1927, também desenvolveram uma teoria relacionando o surgimento de uma epidemia ao valor crítico do número de indivíduos suscetíveis. Juntos publicaram uma série de três trabalhos chamados “Contributions to the mathematical theory of epidemics” [Kermack & McKendrick, 1927], em que estudavam modelos epidemiológicos determinísticos. A teoria do valor crítico é um dos marcos nos estudos da epidemiologia moderna. O valor crítico está relacionado com o número básico de reprodução $R_0 $, que é definido como o número médio de infecções secundárias produzidas quando um indivíduo infectado é introduzido em uma população inteiramente suscetível [Kelling & Grenfell, 2000]. Por exemplo, se $R_0=3$ significa que na média um indivíduo infectado transmiti a doença para outras três pessoas. Portanto, quando temos $R_0 < 1$, o número de infectados tende a zero e a doença se extingue. Se $\displaystyle R_0 > 1$, o número de infectados aumenta e se torna uma epidemia. Este parâmetro tem grande importância na epidemiologia, pois o esforço de se controlar ou erradicar uma doença está intimamente relacionado a ele.
Além no $R_0$ há um outro conceito conhecido como número efetivo de reprodução $R_t$. Ele é definido como o número médio de infecções secundárias produzidas por cada pessoa infectada em uma população que não é inteiramente suscetível, ou seja há pessoas na população que podem possuir imunidade a doença [Vynnycky & White, 2010]. Atualmente segundo o estudo do Imperial College de Londres o número efetivo de reprodução da COVID-19 no Brasil é 2.81 [Short-term forecasts of COVID-19 deaths in multiple countries].
Quem tiver interesse em mais referências e entender melhor sobre epidemiologia matemática, recomendo três vídeos:
- A aula do Professor Evandro Marquesone da UTFPR sobre Epidemiologia Matemática;
- A live da Professora Claudia Pio Ferreira da UNESP sobre Modelagem matemática da COVID-19 ;
- E uma outra aula (em inglês) do Pesquisador Robin Thompson da Universidade de Oxford sobre How do mathematicians model infectious disease outbreaks?
A seguir, apresento um modelo interativo no qual é possível modificar os parâmetros para visualizar o comportamento da dinâmica dos indivíduos e do valor do $R_0 $.